Esta regla recibe su nombre en honor al matemático francés del siglo XVII Guillaume François Antoine, marqués de l'Hôpital (1661 - 1704), quien dio a conocer la regla en su obra Analyse des infiniment petits pour l'intelligence des lignes courbes (1692), el primer texto que se ha escrito sobre cálculo diferencial, aunque actualmente se sabe que la regla se debe a Johann Bernoulli, que fue quien la desarrolló y demostró.
La regla de L'Hôpital es una consecuencia del Teorema del valor medio de Cauchy que se da sólo en el caso de las indeterminaciones del tipo
 ó
ó 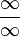 .
.Sean f y g dos funciones definidas en el intervalo [a,b], y sean f(c)=g(c)=0, con c perteneciente a (a,b) y g'(x)≠0 si x≠ c .
Si f y g son derivables en (a,b), entonces si existe el límite f'/g' en c, existe el límite de f/g (en c) y es igual al anterior. Por lo tanto,
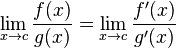
 entre las variables x e y:
entre las variables x e y:
 , implícita, si queremos calcular la derivada de y respecto de x:
, implícita, si queremos calcular la derivada de y respecto de x:  .
. es una función en términos de la variable independiente x y
es una función en términos de la variable independiente x y  es una función en términos de la variable dependiente y, dado que
es una función en términos de la variable dependiente y, dado que 





 x
x