Funciones monotonas (definicion y ejemplo)

Una funcion entre conjuntos ordenados se dice monotona (o isotona) si conserva el orden dado. En calculo se habla de funciones monotonamente crecientes y monotonamente decrecientes (o simplemente crecientes y decrecientes), en la teoria del orden, se usan los terminos monotona y antitona, o se habla de funciones que conservan e invierte el orden.

La funcion f es monotona si y solo si x=y implica f(x)<f(y) (es decir, la funcion es creciente), ó bien x<y implica f(x)>f(y) (es decir, la funcion es decreciente). En otras palabras, una funcion es monotona si conserva el orden.

Nota:
Cuando no tiene concavas se puede decir que son monotonas, ya que no son momentaneamente crecientes o decrecientes.

Cuando tiene concavas se puede decir que es una funcion no monotona.

Funcion monotona creciente:



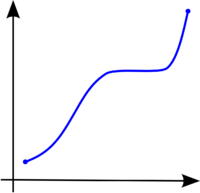
Funcion monotona decreciente:

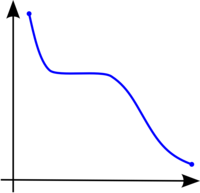
 Funcion no monotona: